Binary Tree
Binary Tree is a data structure extended from linked list data structure. It has the character of inconsecutive data storage , and indirect data access(unlike array’s direct access). It suits to traverse by recursion.
When we traverse a binary tree, we will visit each node twice, once along the top-down direction, once along the bottom-up direction. The node is actually a pointer to access each element on the tree.
Top-down:
- Along the top-down direction, we often run operations before subtrees’ recursive call. The operations often save some data from ancestor’s nodes and use it after subtrees’ return when we visit the node again in the bottom-up direction. Those data is often saved as local variables. If we want to update any variable permanently during a top-down visit, we need to save the variable as an object’s property or an element of a list.
- The (local or global) variable will only be updated when it is satisfied with the question’s requirements. We don’t need to consider what needs to be updated to when the variable is not satisfied with the requirements. If the variable is not satisfied with the requirement, we can choose not to update it.
Bottom-up:
- Along the bottom-up direction, we often run operations after subtrees’ recursive call. The operations are often used to get the final result. The result can be updated in two ways,
- We can save the result in the return type. This way is actually as a conquer operation. Since binary tree naturally separates the problem into left and right subproblems, we can say this way as divide and conquer.
- We also can save the result as an object’s property or an element of a list, similarly to a top-down permanent variable. We use this way to collect the final result is usually because we can not get some intermediate result when we traverse along top-down direction. That is to say, we often apply this bottom-up traversal on intermediate result.
- The result has always to be updated using divide and conquer method , no matter whether the result qualified with the question’s requirement or not. That is because every subtree needs to have a return result even when the result is not updated. Therefore, we need to consider what to return when the result doesn’t need any update. We can think from situations,
- Both left and right subtree has qualified result.
- Left or right subtree has a qualified result, but the other subtree doesn’t. Here we need to consider what needs to be returned when the result is not qualified with the requirement.
- Neither left or right subtree has a qualified result. Here we need to consider what needs to be returned when the result is not qualified with the requirement.
When to use bottom-up and when to use top-down?
-
If a question requires operations differently on left and right subtrees, we can only run those operations along the top-down direction. Only along the top-down direction we can tell a node is on a left or right subtree, but not along the bottom-up direction.
-
If the final result only needs left or right subtree’s result, top-down or bottom-up will both work.
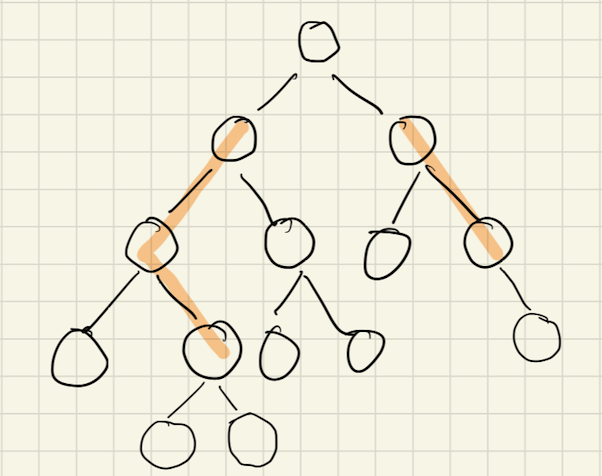
-
If the final result needs to visit left and right subtree at the same time, we can use top-down method with 2 pointers.
-
If the final result needs both left and right subtree’s result, bottom-up method is easier to solve the problem. For example, if we need to get all path sums of a tree, and the path needs to cross a node from the node’s left side to its right side as showing in the below picture, bottom-up method can resolve the issue easily but top-down method will be hard.